Frequencies and thermochemistry
In this tutorial we show how to calculate frequencies of molecules with MLatom. We will basically continue from geometry optimization tutorial, as it is a common practice to first optimize geometry and then calculate its frequency, i.e., to check whether it is a true minimum or transition state (number of imaginary frequencies) and obtain ZPVE and other thermochemical corrections.
Warning
We recommend to use UAIQM methods for these calculations, example below is just to show that you can use other methods too.
Here is a video of frequency and thermochemistry calculations using XACS cloud and Python API:
We start with the same example as that in the beginning of geometry optimization tutorial. Geometry optimization is typically needed before calculating frequencies and the same method or model should be used for both.
After getting the optimized geometry (opt.xyz) as described in the tutorial on geometry optimization, you can do frequency calculations with input file/command line options freq.inp shown below (see the separate section on calculating frequencies via Python API):
freq # 1. requests frequency calculation
ANI-1ccx # 2. pre-trained model, the same as that used in geometry optimization
xyzfile=opt.xyz # 3. file with optimized geometry
Similar to geometry optimization, the user needs to provide the model or method, which can be QM, ML or their combinations. Analytical Hessian is used when it is available, otherwise semianalytical (calculated with analytical gradients) or fully numerical Hessian (calculated with only energies) can be used.
xyzfile=[file name] tells MLatom in what file it can find the geometry. The user can directly use the optimized geometry output by MLatom (file defined by optxyz keyword), or provide it in XYZ format, e.g., for this example (in Angstrom, e.g., opt.xyz) which would look like:
9
C -1.2121068029534 -0.2252488537660 0.0000164117920
H -1.2701429633537 -0.8599818439347 -0.8855315546559
H -1.2701264459840 -0.8599834499240 0.8855643352209
H -2.0710636368970 0.4504289041619 0.0000252076803
C 0.0804149514179 0.5556635798575 0.0000041512523
H 0.1395635927681 1.1970970820212 -0.8856250576131
H 0.1395848675981 1.1970854779804 0.8856411245403
O 1.1428329343502 -0.3971737931938 -0.0000106635278
H 1.9796722202817 0.0702558186994 -0.0001121252171
After you created the input file, you can run MLatom, e.g., on XACS cloud, as:
mlatom freq.inp &> freq.out
The program output will be saved in file freq.out.
Alternatively, you can run the same simulation in the command line with the same options:
mlatom freq ANI-1ccx xyzfile=opt.xyz
You should be able to find in the MLatom output the vibration analysis and thermochemistry results. The vibration analysis prints out frequency, reduced mass and force constant of each normal mode. The thermochemistry part prints out zero-point energy, enthalpy, Gibbs free energy, heat of formation and other properties. For our example, the part of the output would look like:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
Rotational symmetry number: 1
This is a nonlinear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 261.0407 1.0929 0.0439
2 286.9474 1.1295 0.0548
3 428.0328 2.7260 0.2943
4 841.1644 1.0947 0.4564
5 928.2688 2.3346 1.1853
6 1082.6338 3.1779 2.1946
7 1138.6399 1.9583 1.4959
8 1212.5257 1.5518 1.3442
9 1287.5002 1.1134 1.0874
10 1292.8263 1.0682 1.0520
11 1426.7497 1.2307 1.4760
12 1457.4408 1.3203 1.6524
13 1496.9454 1.1496 1.5178
14 1501.2654 1.0458 1.3887
15 1524.8936 1.0529 1.4426
16 3063.7060 1.0530 5.8232
17 3076.9020 1.1120 6.2026
18 3093.2039 1.0342 5.8299
19 3201.4189 1.1000 6.6424
20 3213.8757 1.1004 6.6964
21 3741.4822 1.0681 8.8098
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NNs : 0.00063190 Hartree 0.39652 kcal/mol
Energy : -154.89195912 Hartree
ZPE-exclusive internal energy at 0 K: -154.89196 Hartree
Zero-point vibrational energy : 0.08101 Hartree
Internal energy at 0 K: -154.81095 Hartree
Enthalpy at 298 K: -154.80576 Hartree
Gibbs free energy at 298 K: -154.83631 Hartree
Atomization enthalpy at 0 K: 1.21200 Hartree 760.54458 kcal/mol
ZPE-exclusive atomization energy at 0 K: 1.29301 Hartree 811.37653 kcal/mol
Heat of formation at 298 K: -0.09030 Hartree -56.66187 kcal/mol
Note
MLatom will dump molecule objects in json files named freq[molecule number].json for each molecule containing information from the frequency calculations such as normal modes, frequencies, thermochemistry data.
Visualizing vibrations
There are several ways to visualize the vibrations:
Currently only on the XACS cloud computing:
At the end of the calculations via input file/command line using the options
freq,ir, orraman, MLatom will dump thefreq_gaussian{mol_index}.logfile, which uses Gaussian-style output format for frequencies. You can open it in ChemCraft.You can also dump text output file using Gaussian-style format for frequencies from the Python API:
mymolecule.dump(filename='gauss.log', format='gaussian').
You can directly view the vibrations in
Jupyter notebookby usingmymolecule.view(normal_mode=...), as shown below for an examplemolvibr.jsonfile:
import mlatom as ml
# let's load the molecule with the required properties
molvibr = ml.molecule()
molvibr.load(filename='molvibr.json')
# choose the normal mode to visualize
normal_mode = 1
# let's view it
molvibr.view(normal_mode=normal_mode)
You appear to be running in JupyterLab (or JavaScript failed to load for some other reason). You need to install the 3dmol extension:
jupyter labextension install jupyterlab_3dmol
# we can also check the information for this normal mode
print(f'Frequency: {molvibr.frequencies[normal_mode]:.2f} cm^-1')
print(f'Normal mode in Angstrom')
for atom in molvibr.atoms:
disp = atom.normal_modes[normal_mode]
print(f" {disp[0]:8.3f} {disp[1]:8.3f} {disp[2]:8.3f}")
Frequency: 288.70 cm^-1
Normal mode in Angstrom
-0.000 0.000 -0.025
-0.085 0.168 -0.141
0.085 -0.168 -0.141
0.000 0.000 0.184
-0.000 -0.000 -0.003
0.018 -0.021 -0.014
-0.018 0.021 -0.014
0.000 0.000 0.085
-0.000 -0.000 -0.890
# the non-displaced geometry for reference
print(molvibr.get_xyz_string())
9 C -1.2121068000000 -0.2252488500000 0.0000164100000 H -1.2701429600000 -0.8599818400000 -0.8855315500000 H -1.2701264500000 -0.8599834500000 0.8855643400000 H -2.0710636400000 0.4504289000000 0.0000252100000 C 0.0804149500000 0.5556635800000 0.0000041500000 H 0.1395635900000 1.1970970800000 -0.8856250600000 H 0.1395848700000 1.1970854800000 0.8856411200000 O 1.1428329300000 -0.3971737900000 -0.0000106600000 H 1.9796722200000 0.0702558200000 -0.0001121300000
# non-displaced geometry
molvibr.view()
You appear to be running in JupyterLab (or JavaScript failed to load for some other reason). You need to install the 3dmol extension:
jupyter labextension install jupyterlab_3dmol
Choosing the method or model
The user can benefit from MLatom’s many choices of the methods or models. Many methods such as ANI-1ccx or AIQM1 are recognized automatically by MLatom as shown above. We also show examples of using QM method (B3LYP/6-31G*) and user-trained ML model (ANI model).
The general way to define the QM method is to use method and the corresponding QM program providing its implementations (MLatom uses interfaces to such programs). For example, the input file of using B3LYP/6-31G*:
freq # 1. requests frequency calculation
method=B3LYP/6-31G* # 2. requests running DFT calculation with B3LYP
qmprog=PySCF # 3. requests using PySCF for B3LYP calculations; qmprog=Gaussian can also be used
xyzfile=opt.xyz # 4. file with optimized geometry
The general way to request the frequency calculations with the user-trained ML model is to specify the ML model type with MLmodelType and MLmodelIn keyword. For example, the input file of using ANI model:
freq # 1. requests frequency calculation
MLmodelType=ANI # 2. request optimization with the ANI-type of machine learning potential
MLmodelIn=ani.npz # 3. the file with the trained model should be provided, here it is ani.npz file
xyzfile=opt.xyz # 4. file with optimized geometry
The advanced user-defined hybrid models such as delta-learning models can be used for frequency calculation only via Python API as demonstrated separately.
Note
In principle, our default recomendation is to use AIQM1 as it is usually the most accurate method for affordable cost. However, it is currently only applicable to the compounds with CHNO elements. Another limitation is that to unlock its full potential, we recommend to install the MNDO program for its QM part. The XACS cloud uses Sparrow instead, which currently only provides numerical gradients and Hessians severly limiting its applicability for frequency calculations. ANI-1ccx is hence a good alternative on the XACS cloud if it can be applied (it has additional limitations to neutral closed-shell compounds in ground state).
Also, currently, among ML models, Hessians are currently available only for ANI-type models.
Calculations of many molecules
MLatom can also perform frequency calculations of many molecules like geometry optimization. MLatom will output the vibration analysis and thermochemical properties of each molecule.
To do these calculations, you simply need to prepare the XYZ file with the geometries of multiple molecules (or get this file from MLatom’s previous geometry optimization calculations), e.g., for the hydrogen and methane molecules your opt.xyz file may look like:
2
1 0.0000000000 0.0000000000 0.0000000000
1 0.7414000000 0.0000000000 0.0000000000
5
C 0.0000000000 0.0000000000 0.0000000000
H 1.0870000000 0.0000000000 0.0000000000
H -0.3623333220 -1.0248334322 -0.0000000000
H -0.3623333220 0.5124167161 -0.8875317869
H -0.3623333220 0.5124167161 0.8875317869
Charge and multiplicity
A quick reminder on how to define the charges and multiplicities of a single or multiple molecules. The input might looks something like:
freq # 1. requests frequency calculation
AIQM1 # 2. AI-enhanced quantum mechanical method 1
xyzfile=opt.xyz # 3. file with optimized geometries
charges=0,1 # 4. charge of the first molecule is 0, of the second is 1.
multiplicities=1,2 # 5. multiplicity of the first molecule is 1, second - 2
Note
It does not make sense to define charges and multiplicities for models like ANI-1ccx which were trained on the neutral closed-shell species.
Choosing the program
MLatom provides several ways (programs) to calculate frequencies and thermochemical properties, similarly to geometry optimizations, the user can choose the program with the keyword freqprog. Three options are available:
freqprog=Gaussian, freqprog=PySCF and freqprog=ASE for using the respective programs.
These are actually different tasks and while they are split in Python API (see below), in input file, when freq is requested, both tasks are performed.
freqprog=Gaussian will perform both tasks with Gaussian and will generate input and output files which the user can modify and inspect. Gaussian’s interface is the most time-tested and hence, robust, but not available on the XACS cloud and needs to be installed by the user locally.
freqprog=PySCF will use PySCF to generate thermochemical properties which is quite robust and also available on the XACS cloud since PySCF is an open-source Python package.
If freqprog=ASE is requested, the ASE is used to calculate thermochemical properties following the frequencies calculations performed either with the improved code based on TorchANI (modified to correctly capture the negative frequency in transition states). Frequencies given by modified TorchANI’s code was also tested by us and available on the XACS cloud.
If no freqprog is provided, by default, MLatom will check whether Gaussian is available and use it, then PySCF and ASE & modified TorchANI combination.
Whatever program you chhose, it is worth checking the instructions below for pitfalls and tips.
ASE
For MLatom version older than 3.1.1, the user should tell ASE whether molecules are linear by using ase.linear keyword. If the molecule is linear, you need to set this value as 1, otherwise it is by default 0. If your input XYZ file has more than 1 molecule, ase.linear=1 makes MLatom assume that they are all linear molecules. You can specify the linearity by, e.g., ase.linear=1,0. For version newer than 3.1.1 (including), MLatom can automatically detect the linearity of molecules so you don’t have to specify explicitly. But you can still do that which will override MLatom’s judgement.
It is also important to specify the symmetry of your molecules by using keyword ase.symmetrynumber. The default one in MLatom corresponds to \(C_1\) point group. You can get the symmetry number by referring to the table below, taken from C. Cramer “Essentials of Computational Chemistry”, 2nd Ed.
Point Group |
Symmetry number |
|---|---|
\(C_1\) |
\(1\) |
\(C_i\) |
\(1\) |
\(C_s\) |
\(1\) |
\(C_{{\infty}v}\) |
\(1\) |
\(D_{{\infty}h}\) |
\(2\) |
\(S_n,n=2,4,6,...\) |
\(n/2\) |
\(C_n,n=2,3,4,...\) |
\(n\) |
\(C_{nh},n=2,3,4,...\) |
\(n\) |
\(C_{nv},n=2,3,4,...\) |
\(n\) |
\(D_n,n=2,3,4,...\) |
\(2n\) |
\(D_{nh},n=2,3,4,...\) |
\(2n\) |
\(D_{nd},n=2,3,4,...\) |
\(2n\) |
\(T\) |
\(12\) |
\(T_d\) |
\(12\) |
\(O_h\) |
\(24\) |
\(I_h\) |
\(60\) |
For example, if your input XYZ file has hydrogen (belongs to \(D_{{\infty}h}\) group) and methane (belongs to \(T_d\) group), the input file should look like this:
freq
ANI-1ccx
xyzfile=opt.xyz
freqprog=ase
ase.linear=1,0
ase.symmetrynumber=2,12
Gaussian
When Gaussian is used, you will see the gaussian.log file which is similar to the common Gaussian output file with the difference, that it will use the MLatom’s model to predict Hessian to perform the frequency calculations. Then you can use your favorite tools to analyze this output as usual for Gaussian, which is a big advantage for the Gaussian users. Here is the input file of using Gaussian to calculate frequencies.
freq
ANI-1ccx
xyzfile=opt.xyz
freqprog=Gaussian
For above example, you can check the MLatom’s output file:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
This is a nonlinear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 264.1253 1.0872 0.0447
2 288.7816 1.1305 0.0555
3 429.1248 2.7295 0.2961
4 840.9571 1.0959 0.4566
5 929.0118 2.3254 1.1825
6 1083.2419 3.1763 2.1960
7 1138.7381 1.9666 1.5025
8 1211.7614 1.5471 1.3384
9 1291.9096 1.0694 1.0516
10 1299.4679 1.1131 1.1074
11 1434.7836 1.2319 1.4941
12 1464.0813 1.3257 1.6743
13 1497.4787 1.1427 1.5097
14 1502.1301 1.0457 1.3902
15 1525.4126 1.0539 1.4449
16 3045.3746 1.0531 5.7544
17 3061.9747 1.1130 6.1482
18 3092.9313 1.0343 5.8295
19 3197.6062 1.0999 6.6261
20 3213.0380 1.1000 6.6905
21 3741.0501 1.0681 8.8073
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NNs : 0.00062817 Hartree 0.39419 kcal/mol
Energy : -154.89196013 Hartree
ZPE-exclusive internal energy at 0 K: -154.89196 Hartree
Zero-point vibrational energy : 0.08100 Hartree
Internal energy at 0 K: -154.81096 Hartree
Enthalpy at 298 K: -154.80578 Hartree
Gibbs free energy at 298 K: -154.83631 Hartree
Atomization enthalpy at 0 K: 1.21202 Hartree 760.55134 kcal/mol
ZPE-exclusive atomization energy at 0 K: 1.29301 Hartree 811.37710 kcal/mol
Heat of formation at 298 K: -0.09032 Hartree -56.67409 kcal/mol
The examples of the full MLatom and Gaussian output files can be downloaded too.
An additional important advantage is that the advanced users can modify the gaussian.com file which contains the input required for geometry optimization with MLatom’s models.
After the gaussian.com file is modified, you can run with it the Gaussian job as usual, e.g., in your system like g16 gaussian.com in command line.
PySCF
Frequency calculation with PySCF works similar with that in Gaussian. We slightly modified source code to make it adaptive to MLatom. By using input as below,
freq
ANI-1ccx
xyzfile=opt.xyz
freqprog=PySCF
you will get the MLatom’s output file:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
This is a nonlinear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 263.8939 1.0878 0.0446
2 288.6910 1.1303 0.0555
3 429.0255 2.7312 0.2962
4 840.8114 1.0961 0.4566
5 928.7823 2.3273 1.1829
6 1082.9072 3.1819 2.1984
7 1138.4541 1.9665 1.5017
8 1211.4647 1.5472 1.3379
9 1291.7699 1.0696 1.0516
10 1299.3247 1.1131 1.1072
11 1434.5579 1.2319 1.4937
12 1463.8316 1.3262 1.6743
13 1497.2788 1.1422 1.5087
14 1501.9697 1.0458 1.3901
15 1525.2540 1.0541 1.4448
16 3045.0585 1.0532 5.7540
17 3061.5892 1.1131 6.1473
18 3092.6304 1.0344 5.8292
19 3197.1933 1.1000 6.6252
20 3212.6500 1.1001 6.6896
21 3740.7180 1.0683 8.8072
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NNs : 0.00062817 Hartree 0.39419 kcal/mol
Energy : -154.89196013 Hartree
ZPE-exclusive internal energy at 0 K: -154.89196 Hartree
Zero-point vibrational energy : 0.08098 Hartree
Internal energy at 0 K: -154.81098 Hartree
Enthalpy at 298 K: -154.80579 Hartree
Gibbs free energy at 298 K: -154.83632 Hartree
Atomization enthalpy at 0 K: 1.21203 Hartree 760.55897 kcal/mol
ZPE-exclusive atomization energy at 0 K: 1.29301 Hartree 811.37718 kcal/mol
Heat of formation at 298 K: -0.09033 Hartree -56.68121 kcal/mol
Calculations through Python API
The Python API provides more flexibility to use more complicated models and build custom workflows.
Below is a workflow of optimizing geometry and calculating frequency (see Jupyter notebook):
import mlatom as ml
# Get the initial guess for the molecules to optimize
initmol = ml.data.molecule.from_xyz_string(''' 9
C -1.2121068029534 -0.2252488537660 0.0000164117920
H -1.2701429633537 -0.8599818439347 -0.8855315546559
H -1.2701264459840 -0.8599834499240 0.8855643352209
H -2.0710636368970 0.4504289041619 0.0000252076803
C 0.0804149514179 0.5556635798575 0.0000041512523
H 0.1395635927681 1.1970970820212 -0.8856250576131
H 0.1395848675981 1.1970854779804 0.8856411245403
O 1.1428329343502 -0.3971737931938 -0.0000106635278
H 1.9796722202817 0.0702558186994 -0.0001121252171''')
# Choose one of the predifined (automatically recognized) methods
mymodel = ml.models.methods(method='ANI-1ccx')
/mlatom/software/miniconda3/lib/python3.11/site-packages/torchani/resources/ /mlatom/software/miniconda3/lib/python3.11/site-packages/torchani/resources/
# Optimize the geometry with the choosen optimizer:
geomopt = ml.optimize_geometry(model=mymodel, initial_molecule=initmol, program='ASE', maximum_number_of_steps=10000)
# Get the optimized molecule
final_mol = geomopt.optimized_molecule
print(final_mol.get_xyz_string())
9 C -1.2121068000000 -0.2252488500000 0.0000164100000 H -1.2701429600000 -0.8599818400000 -0.8855315500000 H -1.2701264500000 -0.8599834500000 0.8855643400000 H -2.0710636400000 0.4504289000000 0.0000252100000 C 0.0804149500000 0.5556635800000 0.0000041500000 H 0.1395635900000 1.1970970800000 -0.8856250600000 H 0.1395848700000 1.1970854800000 0.8856411200000 O 1.1428329300000 -0.3971737900000 -0.0000106600000 H 1.9796722200000 0.0702558200000 -0.0001121300000
# Do vibration analysis and thermochemistry calculation
freq = ml.thermochemistry(model=mymodel, molecule=final_mol, program='PySCF')
# or vibration analysis only
# freq = ml.freq(model=mymodel, molecule=final_mol, program='')
# Save the molecule with vibration analysis and thermochemistry results
final_mol.dump(filename='molvibr.json',format='json')
# Check vibration analysis
print("Mode Frequencies Reduced masses Force Constants")
print(" (cm^-1) (AMU) (mDyne/A)")
for ii in range(len(final_mol.frequencies)):
print("%d %13.4f %13.4f %13.4f"%(ii,final_mol.frequencies[ii],final_mol.reduced_masses[ii],final_mol.force_constants[ii]))
# Check thermochemistry results
print(f"Zero-point vibrational energy: {final_mol.ZPE} Hartree")
print(f"Enthalpy at 298 K: {final_mol.H} Hartree")
print(f"Gibbs Free energy at 298 K: {final_mol.G} Hartree")
print(f"Heat of formation at 298 K: {final_mol.DeltaHf298} Hartree")
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
0 263.8585 1.0877 0.0446
1 288.6962 1.1303 0.0555
2 429.0266 2.7312 0.2962
3 840.8100 1.0961 0.4566
4 928.7816 2.3273 1.1829
5 1082.9074 3.1819 2.1985
6 1138.4535 1.9665 1.5017
7 1211.4598 1.5473 1.3379
8 1291.7733 1.0696 1.0516
9 1299.3241 1.1131 1.1072
10 1434.5579 1.2319 1.4937
11 1463.8294 1.3261 1.6742
12 1497.2782 1.1422 1.5087
13 1501.9029 1.0458 1.3899
14 1525.2521 1.0541 1.4448
15 3045.0578 1.0532 5.7540
16 3061.5866 1.1131 6.1473
17 3092.6302 1.0344 5.8292
18 3197.2113 1.1000 6.6252
19 3212.6491 1.1001 6.6896
20 3740.7179 1.0683 8.8072
Zero-point vibrational energy: 0.08098376608079631 Hartree
Enthalpy at 298 K: -154.8057865062314 Hartree
Gibbs Free energy at 298 K: -154.83632007673512 Hartree
Heat of formation at 298 K: -0.09032742391785184 Hartree
You can compare your results with the output shown above and obtained with the calculations through the input file.
There will be several properties related to thermochemistry listed below that are attributed to the molecule object (in Hartree for energies and Hartree/K for entropy) after calculation:
saved_dict = {#...
'ZPE': 0.080996, # Zero-point energy
'DeltaE2U': 0.085241, # Difference between internal energy and total energy (ZPVE-exclusive)
'DeltaE2H': 0.086185, # Difference between enthalpy and total energy (ZPVE-exclusive)
'DeltaE2G': 0.055654, # Difference between Gibbs free energy and total energy (ZPVE-exclusive)
'U0': -154.810964, # Internal energy at 0 K
'H0': -154.810964, # Enthalpy at 0 K
'U': -154.80672, # Internal energy at 298 K
'H': -154.805775, # Enthalpy at 298 K
'G': -154.836306, # Gibbs free energy at 298 K
'S': 0.00010240004758876359, # entropy
'atomization_energy_0K': 1.2120157100000029,
'ZPE_exclusive_atomization_energy_0K': 1.293011710000003,
'DeltaHf298': -0.0903159176864495 # Heat of formation at 298 K
}
# check out dict:
# final_mol.__dict__
You can retrieve the value of the property by directly calling molecule.property (e.g. molecule.G will return you the Gibbs free energy of the molecule).
final_mol.G
-154.83632007673512
Note
Note that ml.thermochemistry contains both vibration analysis and thermochemistry calculation. If you just want vibrational analysis, you can use ml.freq instead. All the results are saved as the arguments of final_mol.
Calculations with custom hybrid models
Finally, a more advanced example of using a custom delta-learning model, trained on the differences between full configuration interaction and Hartree–Fock energies:
XYZ coordinates, full CI energies and Hartree–Fock energies of the training points can be downloaded here (xyz_h2_451.dat, E_FCI_451.dat, E_HF_451.dat). You can try to train the delta-learning model by yourself. Here, we provide a pre-trained model using ANI delta_FCI-HF_h2_ani.npz.
import mlatom as ml
# Get the initial guess for the molecules to optimize
initmol = ml.data.molecule.from_xyz_file('h2_init.xyz')
# Let's build our own delta-model
# First, define the baseline QM method, e.g.,
baseline = ml.models.model_tree_node(name='baseline', operator='predict', model=ml.models.methods(method='HF/STO-3G', program='pyscf'))
# Second, define the correcting ML model, in this case the ANI model trained on the differences between full CI and HF
delta_correction = ml.models.model_tree_node(name='delta_correction', operator='predict', model=ml.models.ani(model_file='delta_FCI-HF_h2_ani.npz'))
# Third, build the delta-model which would sum up the predictions by the baseline (HF) with the correction from ML
delta_model = ml.models.model_tree_node(name='delta_model', children=[baseline, delta_correction], operator='sum')
# Optimize the geometry with the delta-model as usual:
geomopt = ml.optimize_geometry(model=delta_model, initial_molecule=initmol, program='ASE')
# Get the final geometry approximately at the full CI level
final_mol = geomopt.optimized_molecule
print('Optimized coordinates:')
print(final_mol.get_xyz_string())
final_mol.write_file_with_xyz_coordinates(filename='final.xyz')
# Let's check how many full CI calculations, our delta-model saved us
print('Number of optimization steps:', len(geomopt.optimization_trajectory.steps))
# Calculate frequency
freq = ml.freq(model=delta_model, molecule=final_mol, program='')
# Check vibration analysis
print("Mode Frequencies Reduced masses Force Constants")
print(" (cm^-1) (AMU) (mDyne/A)")
for ii in range(len(final_mol.frequencies)):
print("%d %13.4f %13.4f %13.4f"%(ii,final_mol.frequencies[ii],final_mol.reduced_masses[ii],final_mol.force_constants[ii]))
Given an initial geometry h2_init.xyz, you will get the following output when using the codes above.
Optimized coordinates:
2
H 0.1272159900000 0.0000000000000 0.0000000000000
H 0.8727840100000 0.0000000000000 0.0000000000000
Number of optimization steps: 7
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
0 4327.2885 1.0078 11.1190
Thermochemistry in Diels–Alder reaction
By using these thermochemical properties, you can easily evaluate relative energies for various aspects of chemical behavior,
such as the change of energy profile during reaction process. We take the Diels–Alder reaction of cyclopentadiene and maleimide, an example in the MLatom 3 paper. You can download the geometry file needed here: re.xyz.
There are 3 structures in re.xyz: the first two strucutres are reactants and the third one is the product (see figure below):
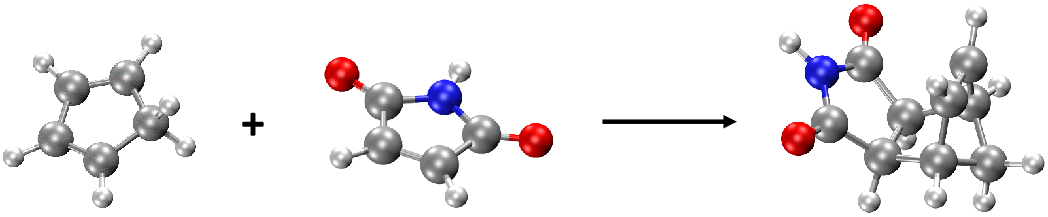
Thus, the basic idea here is that we will calculate thermochemical properties for each molecule and then calculate the energy changes from product to reactants. We will illustrate that it is very convenient to do with the Python API (the same can be done manually through input file/command line calculations by performing thermochemical calculations for each molecule and get the changes in each type of energy).
import mlatom as ml
# read molecules from .xyz file
reDB = ml.data.molecular_database().read_from_xyz_file('re.xyz')
optreDB = ml.data.molecular_database()
# define method to calculate thermochemical properties
model = ml.models.methods(method='AIQM1', qm_program='mndo')
for mol in reDB:
# geometry optimization
geomopt = ml.optimize_geometry(model=model, initial_molecule=mol, program='gaussian')
optmol = geomopt.optimized_molecule
# frequency calculation
ml.thermochemistry(model=model, molecule=optmol)
optreDB.append(optmol)
# get relative energies
deltaE = optreDB[2].energy - optreDB[1].energy - optreDB[0].energy
deltaG = optreDB[2].G - optreDB[1].G - optreDB[0].G
deltaH = optreDB[2].H - optreDB[1].H - optreDB[0].H
print(deltaE)
print(deltaG)
print(deltaH)
Here is the summary of the output containing changes in ZPVE-exclusive energy, Gibbs free energy, and enthalpy.
Method |
\(\Delta E_r\) |
\(\Delta G_r\) |
\(\Delta H_r\) |
|---|---|---|---|
reference |
-34.20 |
- |
- |
AIQM1 |
-34.13 |
-15.98 |
-30.36 |
This shows that if you can use AIQM1, you should use this method to obtain accurate results fast; it is often much more preferable than performing analogous, slower and less accurate, DFT calculations.
Any questions or suggestions?
If you have further questions, criticism, and suggestions, we would be happy to receive them in English or Chinese via email, Slack (preferred), or QQ (135258964). See our contact page for more information on how to subscribe to updates and follow us on social media.